Ecuaciones lineales

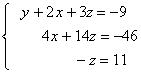
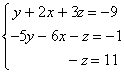
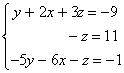
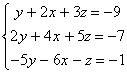
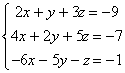
Método de Gauss
El método de Gauss para la resolución de sistemas lineales se puede considerar como un generalización del de reducción (para los sistemas con dos o tres incógnitas). En esencia consiste en hacer, al sistema de ecuaciones lineales, determinadas transformaciones elementales a fin de obtener un sistema escalonado, más fácil de resolver.
Lo explicaremos utilizando un ejemplo:
Ejemplo 11. Consideremos el sistema :
En primer lugar cambiamos el orden de las incógnitas x e y (pues el coeficiente de y es 1, y nos servirá de “pivote”), el sistema queda:
Multiplicamos la 1ª ecuación por 2 y se la restamos a la segunda:
Permutamos las ecuaciones 2ª y 3ª:
Multiplicamos la 1ª ecuación por 5 y se la sumamos a la 2ª:

que es un sistema escalonado.
Hasta aquí es el método de Gauss, ya se ha conseguido un sistema escalonado ahora para resolverlo se procede:
z=-11, de donde
4x = -46-14(-11)Þ x=54/2, la y la obtenemos sustituyendo estos dos valores en la ecuación 1ª ;
y =-9-54+33, y=-30.
La solución es: (54/2,-30,-11)
El método se puede generalizar al caso de m ecuaciones con n incógnita, y se puede llegar a enunciar el siguiente:
Teorema . Todo sistema de m ecuaciones con n incógnitas, puede reducirse a un sistema equivalente del tipo:
(Se harían cero los coeficientes necesarios hasta dejarlo escalonado usando el método de Gauss que se ha indicado en el ejemplo)

ESTUDIO DE SISTEMAS DE ECUACIONES LINEALES
Para el estudio de sistemas de ecuaciones lineales empleamos dos herramientas matemáticas que nos van a facilitar los cálculos : las matrices y los determinantes.
Las matrices y los determinantes nos permiten expresar de una manera clara, concisa y elegante la condición de compatibilidad de los s

istemas de ecuaciones lineales (s.e.l.) - Teorema de Rouché-Fröbenius -.

Preliminares :
La ecuación 2x - 3 = 0 se llama ecuación lineal de una variable. Obviamente sólo tiene una solución.La ecuación -3x + 2y = 7 se llama ecuación lineal de dos variables. Sus soluciones son pares ordenados de números. Tiene infinitas soluciones que se obtienen despejando una variable y dando valores cualesquiera a la otra.La ecuación x - 2y + 5z = 1 se llama ecuación lineal de tres variables. Sus soluciones son ternas ordenadas de números. Tiene infinitas soluciones que se obtienen despejando una variable y dando valores cualesquiera a las otras dos.
En general, una ecuación lineal de "n" variables es del tipo :
Las soluciones son las secuencias de números s1, s2, s3, ..., sn que hacen verdadera la igualdad [1]
Si los coeficientes valen 0 y el término independiente no, la ecuación se llama incompatible. No tiene solución y también se denomina ecuación imposible, proposición falsa o igualdad absurda.
Si los coeficientes y el término independiente son nulos, se dice que la ecuación es una identidad.
Sistemas de Ecuaciones Lineales :
Muchos problemas de la vida real nos obligan a resolver simultáneamente varias ecuaciones lineales para hallar las soluciones comunes a todas ellas. También resultan muy útiles en geometría (las ecuaciones lineales se interpretan como rectas y planos, y resolver un sistema equivale a estudiar la posición relativa de estas figuras geométricas en el plano o en el espacio).
Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales que podemos escribir de forma tradicional así :

Este mismo sistema de ecuaciones lineales en notación matricial tiene esta forma :

Dode :
Llamamos matriz del sistema a la matriz de dimensión m×n formada por los coeficientes del sistema, y la designamos por A.
Designamos por X a la matriz columna formada por las incógnitas.
Denotamos por B a la matriz columna formada por los términos independientes.
y llamamos matriz ampliada de dimensión m×(n+1) a la matriz que se obtiene al añadir a la matriz del sistema (= matriz de coeficientes) la columna de los términos independientes, y la denotamos por A*, es decir

Clasificación :
Atendiendo a sus soluciones :

Ejercicios

POTENCIA Y RAIZ

Potencias y raíces de números complejos
La operación de la potenciación en los números complejos se simplifica mucho si se recurre a la representación gráfica de estos números en el plano cartesiano. Si , se identifica a con el par ordenado y se representa como un punto en el plano cartesiano de la manera usual (ver figura de la derecha).


También puede representarse como el vector con origen en el punto y extremo en el punto . (ver figura de la izquierda)
El módulo de un número complejo se define como la longitud del vector del plano que se obtiene como su representación gráfica. Se denota: módulo de Si , Esta representación gráfica permite obtener otra forma de determinar a un número complejo dado. Es la llamada forma trigonométrica o forma polar. Dado el número complejo , representado por el vector del plano cartesiano, se observa que ese vector queda totalmente determinado por 2 datos:

El ángulo que forma el vector con el eje de las abscisas, medido en sentido contrario a las agujas del reloj.
El módulo de

Si sólo se conoce el dato del ángulo que forma un número complejo con el eje de las abscisas, sólo se sabe que dicho número será alguno de los vectores que están en la semirrecta de la figura de la izquierda.
Por otra parte, si de un número complejo , se conoce sólo el módulo, digamos , sólo se puede asegurar que está en la circunferencia de radio que está centrada en el origen.


Pero si tenemos los dos datos mencionados, hay un único número complejo con esas características. Por ejemplo, si el número complejo forma un ángulo de con el eje de las abscisas y , entonces la representación gráfica de es la que se muestra a la izquierda.